PRESSURE MEASUREMENT
INTRODUCTION: The motion of a compact disc (CD), a ferris wheel, a circular saw blade and a ceiling fan have common factor that is each involves a body that rotates through an axis that is stationary or fixed in some inertial frame of reference. Each object is pivoted at a central point. Rotation occurs at all scales, from the motion of electron in atoms to the motion of entire galaxies. (PRESSURE AND TORQUE RELATION)
TYPE OF MOTION
Motion can be classified in different types. Out of these two are :
*Translatory motion
*Rotational motion
TRANSLATIONAL MOTION: It is a type of motion which takes place along a straight line. When we push an object or pull an object , if it is free to move, moves in the direction of the applied force. This type of motion in which the whole body gets displaced is called translational motion. (PRESSURE AND TORQUE RELATION)
ROTATIONAL MOTION: It is a type of motion which takes place about an axis of rotation when we pedal a bicycle resting on its stand, the crank and the wheel rotate. This is an example of rotational motion. The force applied on the pedal has a turning effect on the wheel. Such forces are analogue of forces in translator motion, but not produce translator motion. Such forces are called turning forces. The body rotates because of the torque it experiences due to these turning forces. (PRESSURE AND TORQUE RELATION)
MOMENT OF FORCE:
The turning effect of a force measured in turns of a physical quantity called torque. The turning effect of a force is called torque (turning force) or moment of force. It is defined as the product of the magnitude of force (F) and the perpendicular distance(r) of the axis from the line of action of the force. Torque is additionally named as the moment of force. It is represented by ϯ( tau). Mathematically, we have
Torque = either force X perpendicular distance from the axis of rotation
OR Torque = either force X lever arm or moment arm
Therefore, mathematically tau = F X r
Units of TORQUE
So the units of torque are the units of force multiplied by the units of distance.
IN SI UNIT : Torque is measured in newton-metre (NM)
IN CGS: Torque is measured in dyne-centimetre ( dyn-cm)
FACTORS OF THE TURNING EFFECT OF FORCE :
When forces are used to open doors, steer or pedal bicycles or turn a tap they are causing turning. The effect that a force has in turning an object around depends on . (PRESSURE AND TORQUE RELATION)
*the size of the force
*the perpendicular or shortest distance between the force line and the pivot (the axis of rotation). Both of these factors are taken into account when measuring the turning effect or moment of force.
Moment of a force= force X perpendicular distance from line of action of force to pivot
PRESSURE
When we apply a force on a body it may act at any angle. When a nail is drven into a block of wood by a hammer the force acts normal or perpendicular to the surface of the nail.
The force acting normally or perpendicular on a surface is called THRUST. Thus, thrust is a vector quantity and is measured in the units of force i.e. newton(N) and kilogram-force(kgf).
When the hammer strikes a sharp nail we find that it readily enters into the wood. The same cannot be said about a blunt nail. The blunt nail just refuses to penetrate the wood although the hammer applies the same force on the nail in both the cases. Inanother words, the thrust acting on the nails is same. Then why does this happen? The answer is pressure. The pressure acting on the two nails is different. Pressure is defined as the thrust acting per unit area of a body. Mathematically, we have
PRESSURE= THURST/ AREA
Pressure is measured as newton per squre metre (Nm-2 ) in SI system. Later this unit has been given a specific name pascal(Pa), in honour of the scientist Blaise Pascal.
The unit pascal is defined as the pressure exerteded on a surface area of one metre squre by a thrust of one newton.
EXAMPLE OF TURNING EFFECT OF FORCE
Common examples of turning effect are based on the concept that for the torque to be a maximum force should be applied at the maximum possible distance from the axis of rotation of the body.
1)THE DOOR—A common example of turning effect of force is opening or closing of a door.
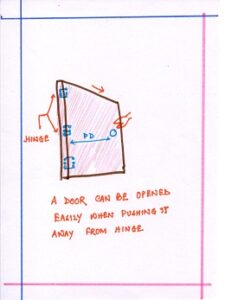
When a force is applied perpendicular to and far away from the hinges of the door then it is easier to open the door. It becomes difficult to open the door if the force is applied closer to the hines; that is why the handle of the door is placed at the end of the door opposite part of the hinge to increase perpendicular distance.
2)THE STEERING WHEEL — In case of the steering wheel the perpendicular distance from the axis of rotation is the radius of the wheel and it is fixed.
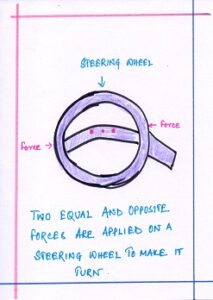
The turning effect or torque is maximum when the forces are applied tangential to the wheel. If the two forces are applied in any one direction, the perpendicular distance between the axis and the force becomes less and torque decreases.
3)A WRENCH— A wrench is another example which utilizes the turning effect of force.

It is used to tighten or loosen nuts. It has a long handle and force is applied at the end which increases the turning effect of force.
EXAMPLES OF THE APPLICATION OF THE CONCEPT OF PRESSURE
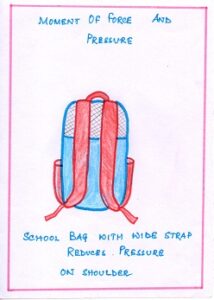
- A school bag has wide strap made of thick canvas. This is done to distribute the entire weight of the bag over a larger area. This in turn will produce a small pressure.
- Knives are ground to this edge. This decreases the area and hence pressure will increase when force is applied on it.
- The tip needle is made sharp so that the force applied on it acts on a small area. This increases the pressure on it and hence it can easily pierce the cloth.
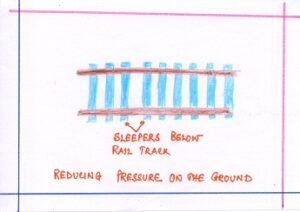
- Wooden or concrete sleepers are placed below the rail lines. This is done to distribute the load
Over a large area, thereby avoidin the sinking the rail line.