ANGLE SUM PROPERTY

INTRODUCTION:

 A plane figure formed by three line segments that are non-parallel to each other is called the triangle.(ANGLE SUM PROPERTY)

 

If A,B,C  are three non-collinear points in the plane of the paper, then the figure made up by the three line segments AB, BC and CA is called a triangle with vertices A,B,C.  The triangle contains three vertices A,B and C and three non-parallel line segments AB,BC and CA. This triangle is denoted by ΔABC.  AB, BC and CA  are sides of ΔABC. Three angles are ˂BAC, <ABC and <ACB.

ELEMENTS or  PARTS: The three sides are  AB, BC, CA and three angles <A, <B, <C of ΔABC are together called the six parts or elements of ΔABC.

INTERIOR and EXTERIOR of  TRIANGLE: We observe that all points in the plane ΔABC are divided into following three parts:

 

 

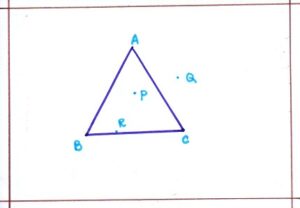
• INTERIOR: The part made up by all such points P which are enclosed by ΔABC is called the interior of ΔABC.
• EXTERIOR: The part made up by all such point Q which are not enclosed by ΔABC is called the exterior of ΔABC.
• TRIANGULAR REGION: The interior of ΔABC  itself includes P and R is called the triangular region ΔABC.

 

                           TYPES OF TRIANGLES

• Naming of triangles by considering the lengths of their sides:-
• Scalene Triangle:

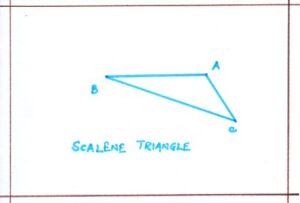
A triangle whose no two sides are equal is called a scalene triangle.  ΔABC is a scalene triangle.

• Isosceles Triangle:

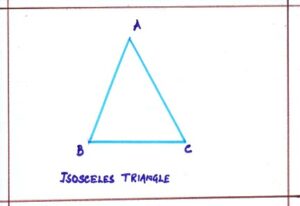
A triangle whose two sides are equal is called an isosceles triangle. ΔABC is an isosceles triangle so AB = AC.

 

• Equilateral Triangle:

A triangle whose all sides are equal to one another, is called an equilateral triangle.  ΔABC is an equilateral triangle where AB = AC = BC.

 

• Naming triangles by considering the measures of their angles:-
• Acute Triangle :

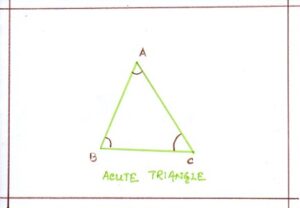
A triangle whose all the angles are acute is called an acute angled triangle or an acute triangle.

ΔABC   is an acute-angled triangle where  <A, <B and < C are acute angles. Equilateral triangle is an acute-angled triangle because the measure of its each angle is 60°.

• Right Triangle:

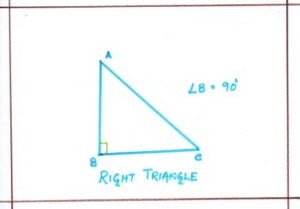
A triangle whose one angle is a right angle, is called right-angled triangle  or a  right triangle.

The side opposite to the right triangle is known as hypotenuse  and other two sides are called the legs of the triangles.

ΔABC  is a right-angled triangle, where <B = 90° remaining two angles are acute.

• Obtuse triangle:

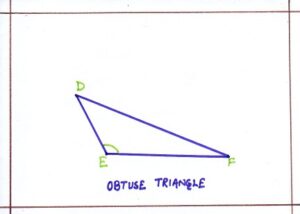
A triangle whose one angle is obtuse, is called an obtuse-angled triangle or an obtuse triangle, where <E  is an obtuse angle.

 

                          ANGLE SUM PROPERTY OF A TRIANGLE

PROPERTY:  The sum of the angles of a triangle is two right angles or 180°

 

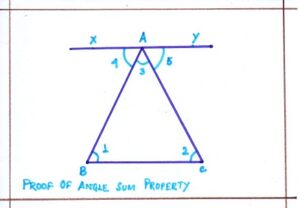
PROOF: Let ΔABC be any triangle. Through A, a line XY parallel to the side BC . Since, XY||BC and the and the transversal AB cuts XY and BC at A  and B respectively.

<1 = <4                              [ as alternate interior angles are equal ]

Similarly , XY ||BC and the transversal AC  cuts XY and BC at A  and C respectively.

<2 = <5                               [ as alternate interior angles are equal]

  Also  <3 = <3

Adding the angles on the respective sides, we get

<1 + <2 + <3 = <4 + <5 + <3

But, <4 + <5 + <3 = 180° = 2 right angles.

Hence, the sum of the angles of a triangle is two right angles or 180°.

From the above property, we obtain the following useful results:-

A triangle cannot have more than one right angle.

A triangle cannot have more than one obtuse angle i.e if one angle of the triangle is obtuse, then other two are acute.

In a right triangle, the other two angles are always acute and their sum is 90°.

 

                               EXTERIOR ANGLE PROPERTY OF A TRIANGLE

PROPERTY:  When a side of a triangle is produced then the exterior angle so formed is equal to the sum of its interior opposite angle.

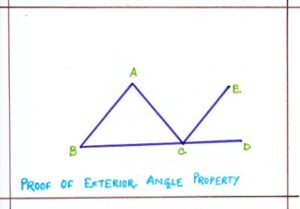
To prove, in ΔABC,  BC has been produced to point D, forming an exterior angle <ACD.

To prove : <ACD = <CAB + < ABC

CONSTRUCTION:  from C, CE is drawn which parallel to BA.

PROOF:  Since  CE||BA and AC is transversal.

So we have <ACE = < CAB                                  [ alternate angle]

Again, CE ||BA  and BCD is a transverse

So, <ECD = <ABC                                                    [corresponding angle]

Adding the corresponding sides

<ACE + <ECD = <CAB + <ABC

<ACD = <CAB + < ABC

Therefore, it is proved that exterior angle of a triangle is always equal to the sum of its interior opposite angle.

 

Let’s discuss some problem on the angle sum property of triangle:

 

Problem 1: Two angles of a triangle measures 63° and 47° respectively. Find the measure of the third angle of the triangle.

 

Solution:  Let the measure of the  third angle be x°; since the sum of all the three angles of a triangle is 180°, we have

63 + 47 + x = 180

Or, 110 + x = 180

Or, x = 180 – 110 = 70

Therefore, the measure of the third angle is 70°

                      

 

Problem 2: The angles of a triangle are in the ratio 2: 3: 4, find the measure of each angle of the triangle.

Solution:  Let  the measures of the given angles be 2x° , 3x° , 4x°,

Since the sum of the angles of a triangle is 180°, so we have : 2x + 3x + 4x = 180

Or, 9x = 180

Or, x = 180/9 = 20

Angles are : 2 X 20 = 40

3 X 20 = 60

4 X 20 = 80

Therefore, the measures of three angles are 40° , 60° , 80°.

Problem 3: Calculate the value of x in the  downward figure. ( what is angle sum property of a triangle)

 

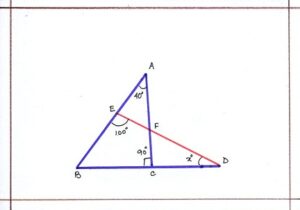
Solution:  In ΔABC,  we have:

<BAC + <ABC + <BCA = 180°

Or, 40°+ <ABC + 90 = 180°

Or, <ABC + 130° = 180°

Or, <ABC = 180 – 130 = 50°

IN ΔBDE , we have:

<EBD + <BDE + < DEB = 180°

Or, <ABC + <BDE + < DEB = 180°

Or, 50° + x° + 100° = 180°

Or, x° + 150°= 180°

Or, x° = 180 – 150 = 30°

Therefore,  the value of x = <DEB = 30°.

Problem 4 : Calculate the value of x in the downward figure.

 

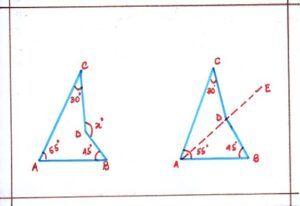
Solution: AD is joined to produce to E.

Since  the exterior angle of a triangle is equal to the sum of interior opposite angles, so

In ΔACD,  <CDE = <DCA + <CAD…………………………(i)

In ΔABD, < EDB = <DAB + <ABD………………………….(ii)

Adding (i) and (ii) , we have;

<CDE + <EDB = <DCA + <CAD + <DAB + <ABD

Or, x° = 30° + (<CAD + <DAB) + 45°

Or, x° = 30° + 55° + 45° = 130°

Or, x° = 130°

Therefore, the value of x = 130°.

Problem 5: In a right triangle, one of the acute angles is 58°. Find the other acute angle.

Solution: Let the measure of the other acute angle be x°, then the angles of the triangle are 90°, 58° and x° .

Since sum of all three angles of triangle is 180◦ according to the angle sum property,

So, 90° + 58° + x° = 180°

Or, 148° + x° = 180°

Or, x = 180 – 148

Or, x = 32°

Therefore, the measure of the other acute angle is 32°.

Problem 6: In the adjoining figure ΔABC is right-angled at <C, and CD ḻ AB , also <A = 65°. Find (i) ACD ; (ii) <BCD; (iii) <CBD.

 

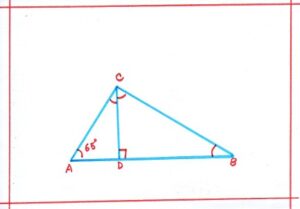
Solution: ΔABC is right-angled triangle,

<C = 90°

<A = 65°

So, <B = 180° – (90° + 65°)

Or, <B = 180 – 155 = 25°

Or, <CBD = 25°

As, CD ḻ AB, Therefore, <ADC = <CDB = 90°

In, ΔACD, we have,

<ACD + <CAD + <ADC = 180°

Or, <ACD + 65°+ 90° = 180°

Or, <ACD = 180 – (90 +65) = 25°

In ΔBCD, we have,

<BCD + <CBD + <BDC = 180°

Or, <BCD + 25° + 90° = 180°

Or, <BCD = 180 – ( 90 + 25)  = 65°

Therefore, <ACD = 25° , <BCD = 65° , <CBD = 25°.

Problem 7: In ΔABC, D,E are points on sides AB and  AC in such a way that DE||BC. If <B = 30° and <A = 40°, find x°,y°, z°. ( what is angle sum property of a triangle)

 

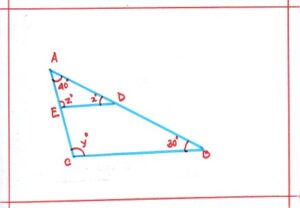
Solution:  In ΔABC, we have,

<A = 40° and <B = 30°

So, <A + <B + <C = 180°

Or, 40°+ 30° + <C = 180°

Or, <C = 180° – (40° +30°)

Or, <C = 110°

DE||BC and transversal AB cuts them at E and c respectively.

<ACB = <AED ……………………. (corresponding angles)

So, y° = z° = 110°

Again, DE||BC and transversal AB cuts them at D and B respectively.

<B = <ADE ………………………….(corresponding angles)

x° = 30°

Therefore, x° = 30° ; y° = 110° ; z° =110°.

Problem 8: This figure has been obtained by using two triangles. Find out <A+<B+<C+<D+<E+<F

 

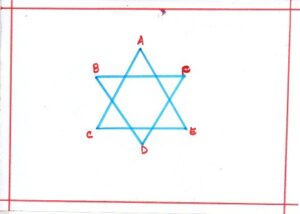
Solution: We know that the sum of the angles of a triangle is 180°

In ΔACE, we have <A +<C+<E = 180°……………..(i)

In ΔBDF, we have <B+<D+<F = 180°………………(ii)

Adding the corresponding sides of (i) and (ii)

We get : <A+<C+<E+<B+<D+<F=  180° + 180°,

So, <A+<B+<C+<D+<E+<F = 360°

Therefore, sum of the six angles are 360°.

 

Problem 9 : Calculate the value of of x.

 

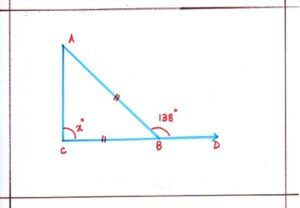
Solution: DBC is a straight line, we have:

<ABD + <ABC = 180°

<ABC = 180 – (<ABD) = 180 – 138 = 42°.

BC = AC = < BAC = <ABC  = 42°.

In ΔABC, we have;

<BAC +<ABC +<BCA = 180°

Or, 42° + 42° + x° = 180°

Or, 84° + x° = 180°

Or, x° = 180 – 84 = 96°

Therefore, value of x = 96°

Problem 10: Calculate the value of x. (what is angle sum property of a triangle)

 

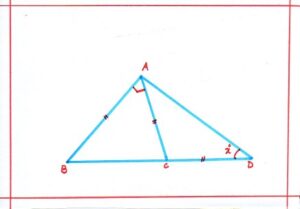
Solution: AB = AC ; so, <ACB = <ABC ………(angles opposite to equal sides of a triangle are equal)

Now, in ΔABC, we have;

<BAC + <ABC +<ACB = 180°

Or, 90°+ 2<ABC = 180°

Or, 2<ABC = 180 – 90

So, <ABC = <BCA = 45°

AC = CD

<CAD = <ADC = x°

Since, exterior angle of a triangle is equal to the sum of interior opposite angles,

So we have <ACB  = <CAD +<ADC = 45°……..( <ACB = x° + x° )

2x° = 45°

Or, x° = (22¹/₂)°

Therefore, the value of x = (22¹/₂)°.